Introduction
The use of computational design methods is increasingly common in landscape architectural education — whether introduced as part of the core curriculum, a studio brief, or explored through a student’s self-guided learning. Yet, in contrast to architectural education, instruction in computational methods is less widespread,1 typically less supported,2 and has fewer resources that cater to the distinct characteristics of landscapes. As a result, the pedagogy of computational design in landscape architectural education remains challenging — even as experience in this area is becoming more widespread in practice and increasingly expected of graduates.3
This paper discusses several approaches for teaching computational design as part of landscape architectural educations and contrasts these approaches with the approaches common to other disciplines. To do so I draw from a diverse range of experience in teaching computational methods across both landscape architecture and architectural programs; in a variety of settings that range from design studios to representation-focused courses to specialised electives; and across experience levels that span from 1st-year undergraduates through to a postgraduate level. While the learning outcomes of each context varies dramatically, these cases employed parametric4 approaches (using the Grasshopper plugin5 for the Rhinoceros modeller) to explore these broader goals using computational methods.
Put briefly, the parametric modelling of geometry allows users to define shapes (and other data) according to specific parameters (say a number, or coordinate) rather than by manually drawing or sculpting a mimetic representation using media such as paper/pencil or the sculptural tools of standard 3D modellers. As a simple example, a user might create a circle parametrically by defining explicit numeric values (i.e. parameters) for its origin point and radius. The resulting circle could then become a parameter for a successive operation (such as creating a column via a vertical extrusion). Modifications to the original circle’s parameters would then automatically affect subsequent operations that depend on them (such as the width of a column). Grasshopper provides a ‘visual scripting’ interface that makes these approaches (relatively) accessible to novice designers through a diagram-like interface for developing a parametric model whereby users place small ‘nodes’ onto a canvas (that represent functions, such as creating a point in space) and ‘wire’ them together to create chains of successive operations (such as creating a point with specific XYZ coordinates or using a series of points to draw a line). This is essentially a visual representation of a data-flow programming paradigm,6 whereby information transfers and transforms in a linear manner to cumulatively develop a more complex model.
Form and Landform
As with any other area of instruction, educators should tailor even a highly-specific teaching goal to the wider curricula and to the abilities and interests of the student cohort. This is especially true for heavily technique-based instruction, such as computational design, which itself has no single clear purpose but can instead accelerate or alter how designers approach a wide variety of design tasks. Nevertheless, there are common threads to the various approaches for introducing computational design methodologies. These span across the enabling software tools used, the design techniques they afford, their relationship to established disciplinary concepts, and how they play into related developments in design technologies such as digital fabrication processes or new methods of site survey. Importantly, in each of these cases, there are distinct differences to the approaches commonly used in architectural education − the typical point of reference for how to teach computational design techniques in the built environment disciplines.
Many of these standard approaches even become counter-productive when deployed within a landscape architectural context. For example, in many landscape projects the design process typically begins with conceptual moves at larger scales and only later proceed to smaller-scale form-making. In contrast, a typical approach to parametric design in architecture encourages beginning design development at a medium-scale (say that of a façade or building section) and progressively developing more detail ‘upwards’ (by combining medium-scale forms that define a building’s envelope or by refining forms in relation to the site context) or ‘downwards’ (by modularising a medium-scale form through smaller levels of formal detail that refine aesthetic or tectonic concerns). Such design moves, when performed parametrically, are more valuable when they can create explicit relationships to the formal aspects of a design that are still in flux. A designer could run a set of shading analytics prior to massing development, but they would become much more valuable when enacted as series of parametric rules that use that very analysis to (for instance) quantitatively evaluate different massing options or automatically optimise formal details such as louvre orientations. Thus the task of defining a building’s envelope — or some other mid-scale attribute — acts as a linchpin design task that can both be informed by initial site analysis and inform subsequent analysis.
Within landscape projects there is usually less of an obvious ‘first-step’ in formal terms that initial analysis and concept design work can pivot towards. Instead, that first-step is something that needs to be itself constructed from working with given site conditions; meaning that when beginning landscape architectural design development parametrically most larger scale site analysis or concept-stage work either precedes the shift to the parametric environment or is itself the prime design task to resolve before a designer proceeds with more ‘formal’ moves that manipulate the site itself.
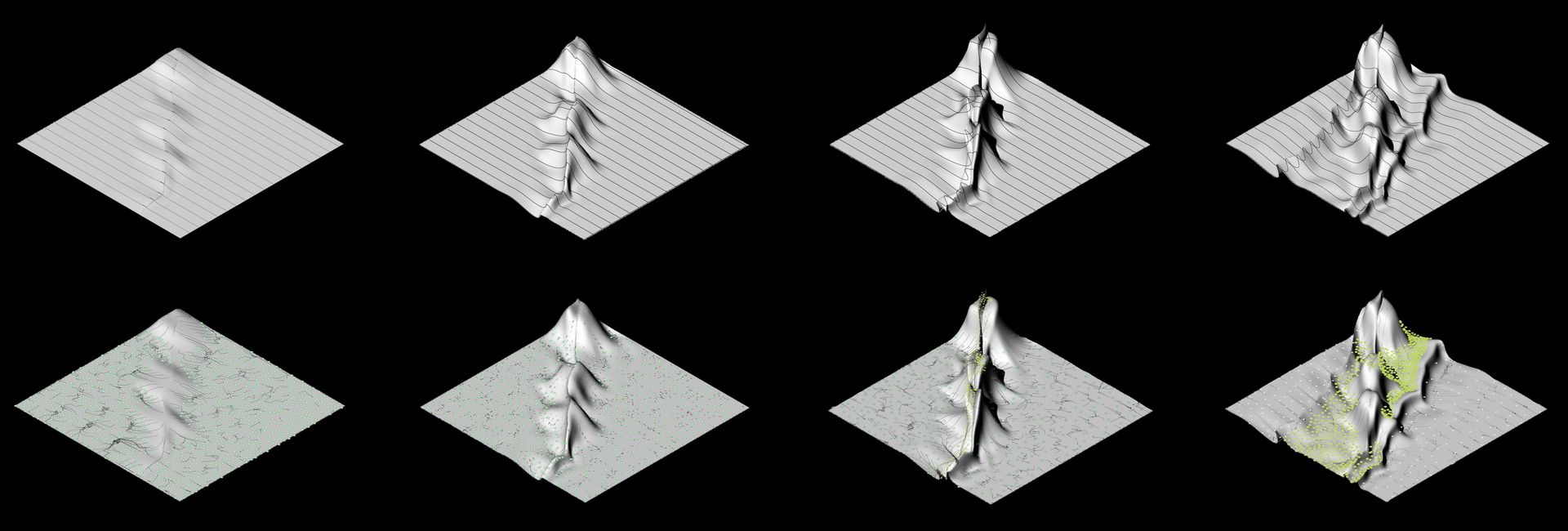
This lack of a formal entry point into design development is seemingly problematic in a parametric modelling environment because most common resources for using Grasshopper and similar tools focus on the use of ‘developable’ Non-Uniform Rational B-Spline geometries (NURBS) as a key means of design development due to their capacity for articulation through the application of pattern and adaptive components to that surface. However, in a landscape context, the reduction of landscape form to that of a plastic NURBS geometry encourages designers to see landscape form and material as a homogeneous and inert entity7 in a manner that runs contrary to the disciplines’ emphasis on dynamism and differentiation. To the extent that a CAD environment represents a site model — say as a NURBS surface in Rhinoceros — the manipulation of that model becomes the obvious ‘first step’ for design development even as those manipulations are largely limited to highly sculptural modifications to a landform whose ‘model’ lacks detailed information about ground cover, soil texture, and innumerable other contextual details that normally inform or enable design decisions.
Re-framing Parameters
In addition to these specific concerns, the broader (apparent) framing of computational design within an architectural context means that it is easily seen as just a method for driving complex form-making and/or performance-driven approaches that simulate the effects of various phenomena on built form. This perspective, left unchallenged, portrays computational methods as alien to a landscape context where these tasks are less prominent. This minimises the potential of computational methods by rendering their applications as responding only to niche concerns. However, alternative framings can provide alternate perspectives that see computational methods through a landscape architectural lens that portrays their value in more expansive terms. Doing so allows students to locate the use of computation in relation to their pre-existing interests within the discipline, which in turn offers them more agency in how they approach the task of learning and adopting new design methods.8 That teaching new — and in many ways unusual — design techniques would benefit from being strongly located within a disciplinary context is of course not surprising. Yet, exactly how to do so in the particular case of landscape architectural applications of computational design methods is not intuitive nor widely supported by accessible education resources.
Successful approaches here seem to, in most cases, involve a re-orientation of the implicit purpose of a typical parametric model: that its primary use is to develop or test geometric details at levels of complexity that are difficult to manage with traditional approaches to analogue or digital modelling. The dynamism inherent to parametric modelling means that the while the end result of a model may be geometric, the process by which that geometry is constructed can be rationalised in a number of different ways. When modelling forms or phenomena in a landscape context, the input or outputs of the model may still be form-dependant but the ways in which those forms are constructed can be framed as a task of understanding landscape processes (be they natural or constructed) and then translating those into geometric representations that explore tendencies rather than fixed outcomes. This contrasts to the standard approach to geometric development where the construction of a formal outcome is designed by an instrumental goal of the designer’s choosing — such as sculpting a visually pleasing composition or rationalising a form into constructable components. For example, processes of erosion can be understood through geometric processes of division and warping whereby the input (initial site topography) and output (projected site topography) can be mediated between by actively constructing parametric relationships that quantify exactly how erosive action impacts landform. In cases such as these, parametric models offer a means to actively explore landscape processes (as is often emphasised in contemporary theory9) in a manner that goes beyond general tendencies, and instead becomes an instrument for specific design exploration due to the explicit yet flexible nature of the parametric model.
Figure .
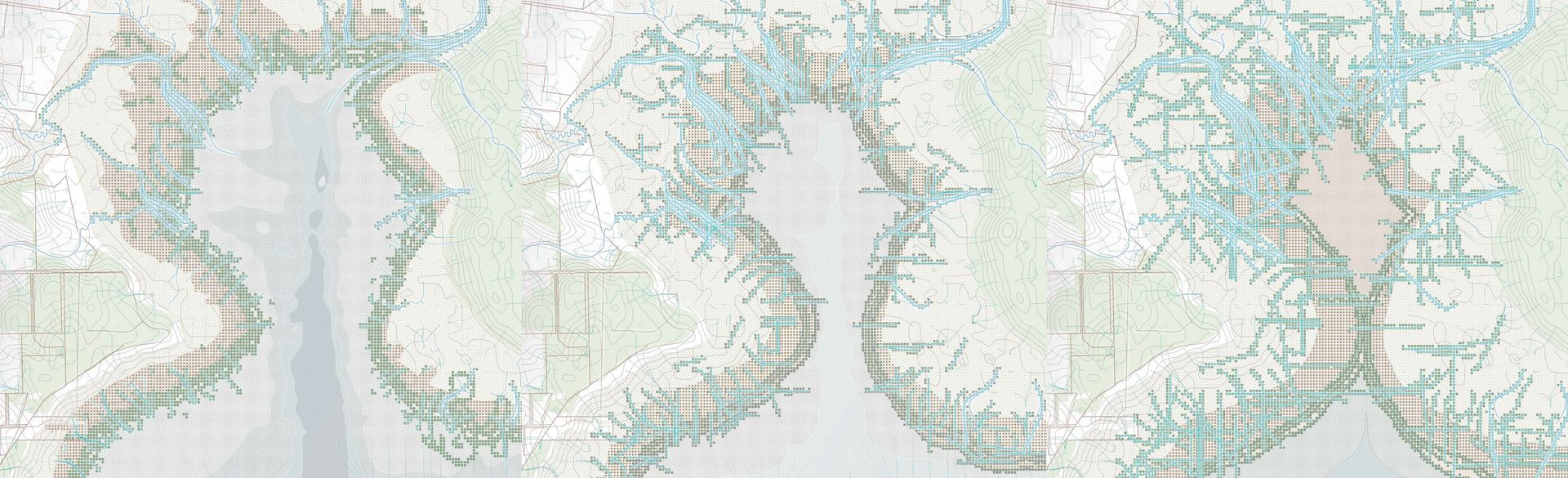
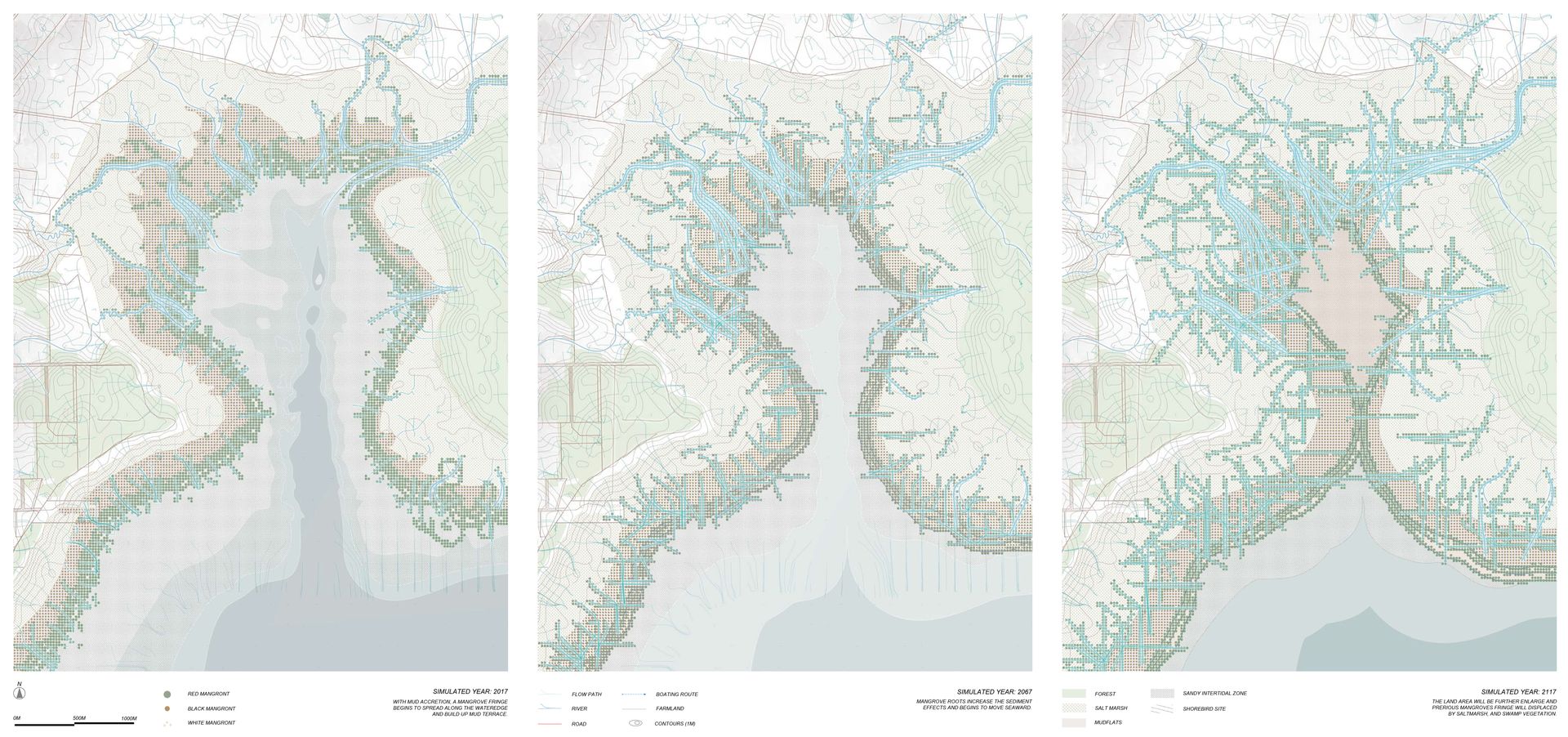
Figure . undefined. Extracts from the work of Louella Exton for the Communications 2 course that is completed as part of the second year of RMIT's Bachelor of Landscape Architectural Design program .
In a similar manner, the parameters that drive the expression of parametric geometries can be seen as not necessarily just capturing design intent (whereby users might ‘dial in’ whatever values create an interesting outcome) but as a means to quantitatively assess site conditions and dynamics by uncovering their specific relationships. Hydrological conditions, such as surface water pooling or flooding, can be examined as a general effect but also refined to specific values derived from site research and observation whereby the exact levels of historic floods can be modelled and used to test the designed outcome. Even better, this offers the chance to go beyond purely ‘layer cake’ approaches to site analysis and instead quantitatively examine the relationships between diverse landscape conditions — such as linking rainfall levels to specific spatial flooding extents — and then use this to extrapolate a more general model.
This capacity for parametric malleability to be understood as not just a means for design exploration but as a model of landscape operations can then be used as a tool for investigating a fundamental aspect of landscapes: time. While modifying of parameters is typically seen as an excise in choosing between design variations or specifying performance attributes, they also provide the means to easily enable cross-temporal representations of how landscapes evolve. In particular, this offers a relatively unique capability of parametric modelling, whereby a model that projects how a site changes over time can be readily constructed by re-organising established geometric relationships in terms of temporal change. As a result, aspects such as plant growth, programmatic intensity, or cut/fill manipulations can be examined not as a single intervention but as a staged and successional series of operations.
Figure .
Figure . undefined. Extracts from the work of Sharon Wu completed as part of the first year of the RMIT's Master of Landscape Architecture program .
Affinities and Overlaps
At the same time, there are many affinities to how computational methods are taught in both an architectural and landscape architectural context. These are worth highlighting to identify where these can overlap with standard landscape architectural curricula and how they can reinforce or re-frame concepts that are explored in other settings that might not seem like natural contexts for introducing computational design techniques. These include:
- A relational approach to design development. The dynamic nature of parametric models ties closely to existing landscape architectural discourse that emphases systems thinking as an approach to understanding site conditions as the result of relationships and feedback cycles between diverse actors. Computational techniques allow for students to explore this approach in a rigorous and explicit manner by not only understanding a system in abstract terms but to begin to quantify those interactions and employ them within design development.10
- A pluralistic approach to approaching design tooling. In the particular context of Grasshopper, there is a thriving software ecosystem of plugins that allows students to look beyond the monolithic software programs common to design education and instead ‘looking for the right tool for the problem.’11 Given our discipline coordinates between a diverse range of actors, having flexibility in adopting new methods can help better understand related fields and encourage collaboration.12
- An emphasis on explicit geometric relationships. While not all designs should exhibit formal complexity, the task of defining complex forms through parametric models is a often a rigorous test of how well students understand geometry and tectonics; particularly when explored alongside fabrication technologies that introduce physical constraints.
Conclusion
Teaching that heavily incorporates digital design methods that depend on software workflows is often characterised as an exercise in ‘skilling’13 or as a more vocational aspect of instruction better confined to external resources such as brief seminars or online videos. While these external resources can be valuable for learning specific concrete tasks, they remove much of the spaced interaction and ad hoc collaboration that drive effective design outcomes.14 They may provide helpful instruction in the mechanical tasks of executing software programs, but then fail (particularly in a landscape architectural context) to detail and develop the distinct conceptual approaches that underpin computational design and are key to understanding its value to the design process beyond a specific task.
Developing this higher-level understanding typically involves the difficult task of first giving students enough of an introduction to this new form of design that they can then locate its value within the discipline15 16 and the wider goals of the course. Many of the pedagogical approaches discussed above can help aid and accelerate this process, while also providing a more critical angle on how many de facto practices and resources for teaching computational design techniques can be ill-suited to landscape architectural purposes. This desire for more discipline specific practices was what drove the release of the “Groundhog”17 project: a Grasshopper plugin and set of online documentation that provides resources (similar to options such as Lynda18 or Designalyze19) explicitly catering to landscape architectural uses and the approaches discussed here. While online resources don’t provide the kinds of highly contextual instruction discussed above, having resources that more explicitly focus on a landscape context will likely serve as useful aids in developing instruction or for students’ own self-directed learning.
That said, any approach to teaching computational design should first reflect critically on any provided resource or tool and look to adapt both its use and framing in terms of a broader learning intent.20 Adapting emerging technologies and approaches in this manner can be difficult, as even with established examples of pedagogical and professional practice it is difficult to distinguish between ‘soft’ and ‘hard’ limitations that stem from de-facto practices and the tools themselves respectively. But doing so allows us to characterise tools, such as computational methods, as a way further in to our discipline21 rather than as a niche curiosity.
- Jillian Walliss et al., “Pedagogical Foundations,” Journal of Landscape Architecture 9, no. 3 (2014): 72.↩
- Jillian Walliss et al., “Pedagogical Foundations,” Journal of Landscape Architecture 9, no. 3 (2014): 72.↩
- Pia Fricker, Christophe Girot, and Georg Munkel, “How to Teach ‘New Tools’ in Landscape Architecture in the Digital Overload,” in Computation and Performance Proceedings of the 31st eCAADe Conference, ed. Rudi Stouffs and Sariyildiz (presented at the eCAADe, Delft, The Netherlands, 2013), 546.↩
- Parametric modelling is but one particular technique within the broader range of computational techniques available. That said Grasshopper allows for advanced students to explore methods such as scripting, agent-based modelling, and evolutionary solvers that go beyond a purely parametric paradigm.↩
- Grasshopper is the predominant ‘computational’ tool used across education and practice settings for 3D design development; a factor driven by its (relatively) intuitive interface and the high amount of extensibility offered by its plugin system and online community.↩
- Daniel Davis, “Modelled on Software Engineering” (Doctoral Thesis, RMIT University, 2013), 101.↩
- Julian Raxworthy, “Novelty in the Entropic Landscape” (Doctoral Thesis, The University of Queensland, 2013), 56.↩
- Stanislav Roudavski, “Selective Jamming: Digital Architectural Design in Foundation Courses,” International Journal of Architectural Computing 9, no. 4 (2012): 440.↩
- Jillian Walliss et al., “Pedagogical Foundations,” Journal of Landscape Architecture 9, no. 3 (2014): 72.↩
- Jillian Walliss et al., “Pedagogical Foundations,” Journal of Landscape Architecture 9, no. 3 (2014): 79.↩
- Daniel Davis, “Modelled on Software Engineering” (Doctoral Thesis, RMIT University, 2013), 126.↩
- Ignacio López Busón et al., “A Computational Approach to Methodologies of Landscape Design,” in Humanizing Digital Reality, ed. Klaas De Rycke et al. (Singapore: Springer Singapore, 2017), 669.↩
- Pia Fricker, Christophe Girot, and Georg Munkel, “How to Teach ‘New Tools’ in Landscape Architecture in the Digital Overload,” in Computation and Performance Proceedings of the 31st eCAADe Conference, ed. Rudi Stouffs and Sariyildiz (presented at the eCAADe, Delft, The Netherlands, 2013), 31.↩
- Robert Zehner et al., “Optimising Studio Outcomes,” in ConnectED 2010 - 2nd International Conference on Design Education, New South Wales, Australia: Connected, 2010), 2.↩
- Pia Fricker, Christophe Girot, and Georg Munkel, “How to Teach ‘New Tools’ in Landscape Architecture in the Digital Overload,” in Computation and Performance Proceedings of the 31st eCAADe Conference, ed. Rudi Stouffs and Sariyildiz (presented at the eCAADe, Delft, The Netherlands, 2013), 546.↩
- Jörg Rekittke and Philip Paar, “Wheeling a Trojan Horse to Teach MLA Students Geoinformation Methods,” in Peer Reviewed Proceedings of Digital Landscape Architecture 2011 (presented at the Digital Landscape Architecture, Anhalt, Germany, 2012), 39.↩
- The site and plugin are currently in a public beta phase with new content being rolled out over the course of 2018.↩
- Lynda is a professional skill-training video company with many courses catering to CAD and other design software.↩
- Designalyse offers a series of instructional videos focused on Rhinoceros and Grasshopper developed by two architects who work across academia and practice.↩
- Jillian Walliss et al., “Pedagogical Foundations,” Journal of Landscape Architecture 9, no. 3 (2014): 83.↩
- Fricker, Girot, and Munkel, “How to Teach ‘New Tools’ in Landscape Architecture in the Digital Overload,” 552.↩